LAMMPS Plastic strain calculation

Posted on | In

LAMMPS This post provides the approach to extract the plastic strain in MD simulation. We can compute the atom displacement as the trajectory from the MD simulation, but the strain is the concept in continuum mechanics, it is really hard to compute the tensor in a discrete system. Recently, some tools provide this function based on a theory that accounting the effects of the neighbor atoms. While considering the relative displacement with the neighbor atom and using the weight function, the deformation gradient tensor can be calculated. Therefore, the strain tensor is obtained. Plastic strain can be expressed as,

\[\boldsymbol{\varepsilon}^p  = \boldsymbol{\varepsilon} - \boldsymbol{\varepsilon}^e\]

so two strain tensor should be generated in the simulation data: total strain tensor $\boldsymbol{\varepsilon}$ and the elastic strain tensor $\boldsymbol{\varepsilon}^e$. Obviously, LAMMPS data file does not provide such information. Here I use the OVITO to get this data.

OVITO provide two modifiers, the first one is the “Atomic strain” and the second one is the “Elastic strain calculation”. Both of them provide the deformation gradient tensor and the strain tensor data. But I found there are some bugs for strain tensor output in OVITO, so I use the deformation gradient tensor data and computing the strain tensor with a Python script.

Let us start by running a Python script with the OVITO interpreter. Get into your OVITO installation folder and find the “ovitos.exe” in this directory. This is the Python interpreter. Actually, OVITO has integrated the Python interpreter, so we do not need to provide an extra Python interpreter. However, there is a drawback of this internal Python interpreter, the package in the internal interpreter just contains the “Numpy” and “Matplotlib”. So if you need the extra function from the Python package. I think you need just use the internal interpreter as the start.

The following image is from the official website of the OVITO documentation. If we get the object of the “ObjectNode”, then we can handle all data and modifiers in the pipeline.

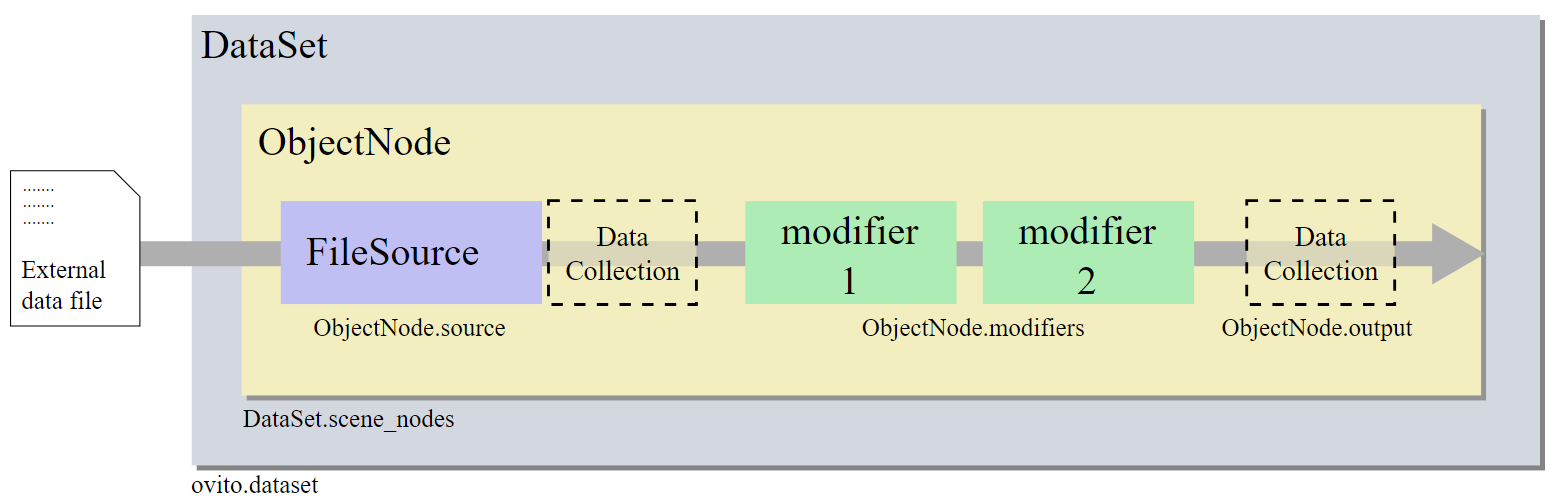
Pipeline

Fortunately, the OVITO import_file function provides access to the “ObjectNode”. Now, we do some basic operations and define some functions before we try to get the deformation gradient tensors.

1
2
3
4
5
6
7
8
9
#Import several modules.
import os
import sys
import numpy as np
try:
    from ovito.io import * #Import the Ovito module
    from ovito.modifiers import *
except:
    pass

This part import several modules and try to import the “ovito.io” module. The Python script can just be run by the “ovitos.exe”, so use try except to avoid the error when running this script directly from the interpreter.

The first function is to form the Voigt notation to a matrix form. You can get more information about the Ovigt notation from the Wikipedia here. In general, since several tensors, such as the stress tensors, strain tensor and stiffness tensor, have symmetric properties,  Voigt notation simplifies the expression to a vector to reduce the computational cost. For example, If we get the principal strain tensor and use Voigt notation to express them, the plastic flow rule can be simplified. Here is the matForm function,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
def matForm(voigtM):
    if type(voigtM) is not np.ndarray: #check the type of voigtM
        sys.exit("matForm: the parameter should be <numpy.ndarray>")
    elif voigtM.ndim != 1: #check the dim of voigtM
        sys.exit("matForm: the parameter should be 1 dimension")
    outputM = np.zeros(shape=(3,3))
    if len(voigtM) == 6: # strain tensor
        outputM[0,0] = voigtM[0]
        outputM[1,1] = voigtM[1]
        outputM[2,2] = voigtM[2]
        outputM[0,1] = voigtM[3]
        outputM[0,2] = voigtM[4]
        outputM[1,2] = voigtM[5]
        outputM[1,0] = voigtM[3]
        outputM[2,0] = voigtM[4]
        outputM[2,1] = voigtM[5]
    if len(voigtM) == 9: #Deformation gradient tensor
        outputM[0,0] = voigtM[0]
        outputM[1,0] = voigtM[1]
        outputM[2,0] = voigtM[2]
        outputM[0,1] = voigtM[3]
        outputM[1,1] = voigtM[4]
        outputM[2,1] = voigtM[5]
        outputM[0,2] = voigtM[6]
        outputM[1,2] = voigtM[7]
        outputM[2,2] = voigtM[8]
    return outputM

Note that the order in OVITO is different from that of the traditional Voigt notation. Usually, Voigt notation treats the order of a strain tensor as,

\[\left( \varepsilon_{11}, \varepsilon_{22}, \varepsilon_{33}, \varepsilon_{23}, \varepsilon_{13}, \varepsilon_{12} \right)\]

but in OVITO, the order will be,

\[\left( \varepsilon_{11}, \varepsilon_{22}, \varepsilon_{33}, \varepsilon_{12}, \varepsilon_{13}, \varepsilon_{23} \right)\]

Then, the following functions define the Almansi tensor and Green tensor,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
def almansiStrain(defGradM):
    almansiStrain = np.zeros(shape=(3,3)) #Start a empty matrix
    identityM = np.identity(3) #Set the identity matrix
    # Get the rank of defGradM
    if np.linalg.matrix_rank(defGradM) != 3: 
        return almansiStrain
    try:
        invdefGradM = np.linalg.inv(defGradM)
    except np.linalg.LinAlgError:
        # Not invertible. Skip this one.almansiStrain
        return almansiStrain
    else:
        almansiStrain = 1.0 / 2.0 * (identityM - \
                        np.dot(np.transpose(invdefGradM),invdefGradM))
    return almansiStrain

def greenStrain(defGradM):
    greenStrain = np.zeros(shape=(3,3))
    identityM = np.identity(3)
    greenStrain = 1.0 / 2.0 * (np.dot(np.transpose(defGradM),\
                  defGradM) - identityM)
    return greenStrain

Green tensor can be written as,

\[{\bf E} = {1 \over 2} \left( {\bf F}^T \cdot {\bf F} - {\bf I} \right)\]

and Almansi tesnor is,

\[{\bf e} = \frac{1}{2} ({\bf I} - {\bf F}^{-T} \! \cdot {\bf F}^{-1})\]

The defination can be found in the continuum mechanics website.

After both elastic strain tensor and the total strain tensor are obtained from the calculation, the plastic strain tensor should be,

1
2
3
4
5
6
def plasticStrain(elasticDefGrad, totalDefGrad):
    #Compute the plastic strain tensor: totalStrain - elasticStrain
    elasticAlmansiStrain = almansiStrain(matForm(elasticDefGrad))
    totalAlmansiStrain = almansiStrain(matForm(totalDefGrad))
    plasticAlmansiStrain = totalAlmansiStrain - elasticAlmansiStrain
    return plasticAlmansiStrain

The last thing here is to turn the matrix form to Ovigt notation since we need to save the plastic strain tensor,

1
2
3
4
5
6
7
8
9
def matStrainToLine(mat):
    voigtForm = np.empty((1,6), float)
    voigtForm[0,0] = mat[0,0]
    voigtForm[0,1] = mat[1,1]
    voigtForm[0,2] = mat[2,2]
    voigtForm[0,3] = mat[0,1]
    voigtForm[0,4] = mat[0,2]
    voigtForm[0,5] = mat[1,2]
    return voigtForm

Now, let us set the working directory and the main function,

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
#######################################################
#Set the parameters
#######################################################
#Set file path.
workDir = "/Users/zhudongping/Documents/Research/Item2/"
inputFileName = "tension.lammpstrj"
outputFrameSeq = list(range(0,85,5))+list(range(3,85,5))
#outputFrameSeq = [43]
atomCutOffDist = 5.5
atomLatticeConst = 2.8665
try:
    atomLatticeType = ElasticStrainModifier.Lattice.BCC
except:
    pass
if __name__ == '__main__':
    try:
        main()
    except:
        print('=================ATTENTION===================')
        print('Please run this script with Ovito interpreter')
        print('=============================================')

All source code is available upon request.