Working with Abaqus explicit calculations recently, I encountered a common issue: the model and materials were fine, and calculations were possible, but the computation speed was extremely slow. With the stable time increment step at the magnitude of $10^{-7}$, even simulating just one second could require thousands of hours of computation, which is impractical. After studying various sources, I’ve summarized methods to accelerate Abaqus explicit calculations.
The stable time increment step is determined by the formula:
\[\Delta t \le f \cdot {\left( {\frac{h}{c}} \right)_{\min }}\]where:
- $h$: The smallest element size;
- $c$: The wave speed;
- $f$: A scale factor for stability;
The wave speed can be calculated using:
\[c = \sqrt{\frac{E}{\rho}}\]where:
- $E$: Elastic modulus;
- $\rho$: Density;
To increase the stable time increment, one can adjust the elastic modulus, density, smallest element size, and the scale factor. The scale factor $f$ is typically set to 0.9 and should generally not be adjusted to avoid affecting result stability. Increasing the element size can improve the stable time increment and reduce overall computational effort, but for complex-shaped models, this may lead to inaccurate results. Adjusting the elastic modulus impacts accuracy, so the practical option is to control material density. However, artificially adjusting material density could cause computational issues, instead, we can use the Abaqus Mass scaling option.
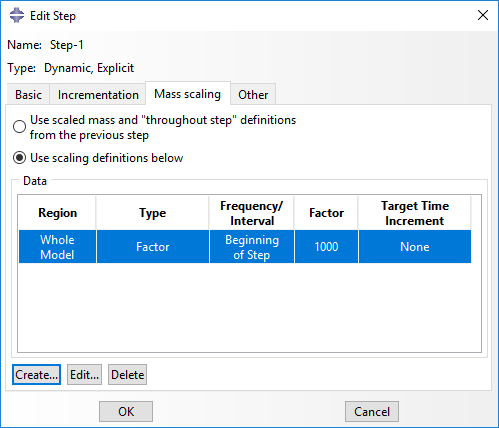
Mass scaling automatically adjusts the mass of some materials in the model to speed up computations. For rate-independent materials in quasi-static analyses, scaling the mass introduces minimal error, but significantly reducing computation time. It is essential that the model kinetic energy remains much lower than its internal energy. For rate-dependent materials and dynamic models, mass scaling can be applied to non-critical areas without significantly affecting the overall mass. For critical areas, mass should only be slightly increased.
Other methods do not increase the stable time increment but can speed up calculations. For instance, parallel computing can enhance speed, but more CPU cores do not always mean better performance. The data exchange between CPUs can slow down calculations, especially if the model is small but many CPU cores are used, leading to longer computation times than single-CPU calculations. Additionally, excessive constraints can reduce Explicit analysis efficiency whether using TIE, COUPLING, MPC, or CONNECTORS. Too many constraints can also prevent Abaqus from parallel computing, resulting in errors like “The requested number of domains cannot be created due to restrictions in domain decomposition.” In such cases, reconsidering and adjusting constraints may improve computation efficiency.