Since my study has something to do with the fatigue under dynamic loading, I have to simulate the crack behavior and its SIF with dynamic effect. Thus, this post analyzes an example including the evolution of crack stress intensity factor under dynamic loading. In the prevous post, we do not have to set the density since the model is under static analysis. However, for dynamic loading, density is critical and should be set correctly
To include the dynamic effect, I still use the following 2D crack model. The width and height of the plate are 1.0 m. The vertical crack is located in the plate center with the length 2a = 0.04 m. The left edge is fixed while a instant stress of 5 MPa. The instant stress duration is 0.001 s, then we continue the analysis until 0.02 s.
The model is shown in the following figure. We simply use PLANE183 element for crack tip simulation. The elastic modulus is 2.1E11 MPa, density is 7800 kg/m^3, and Poisson’s ratio is 0.3. As indicated in the previous post, we have to create two different local coordinate systems, each of which should be located at the crack tip.
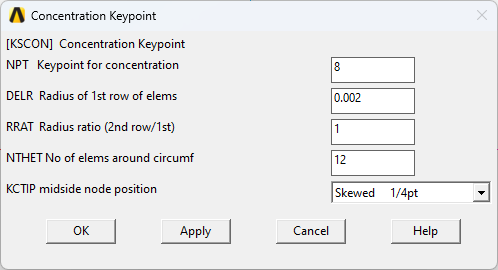
The concentration keypoint setting is shown below,
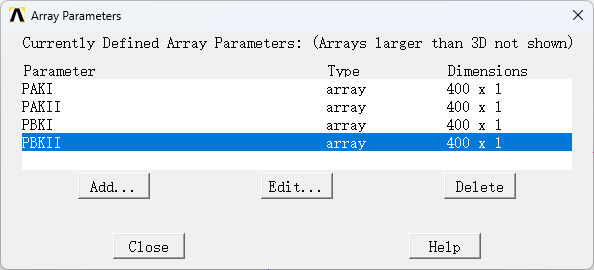
After we finish meshing, we first should create some arrays to store the SIFs during the analysis. Here, I create four arrays with the size of 400 rows so that it is large enough to store SIFs for all steps,
To solve the dynamic loading condition, we should use two loops here. The first loop solves the loading condition from 0 to 0.001 s. THe second loop solves the loading condition from 0.001 to 0.02 s. For each timestep T, we run the solver with the following setting,
1 | |
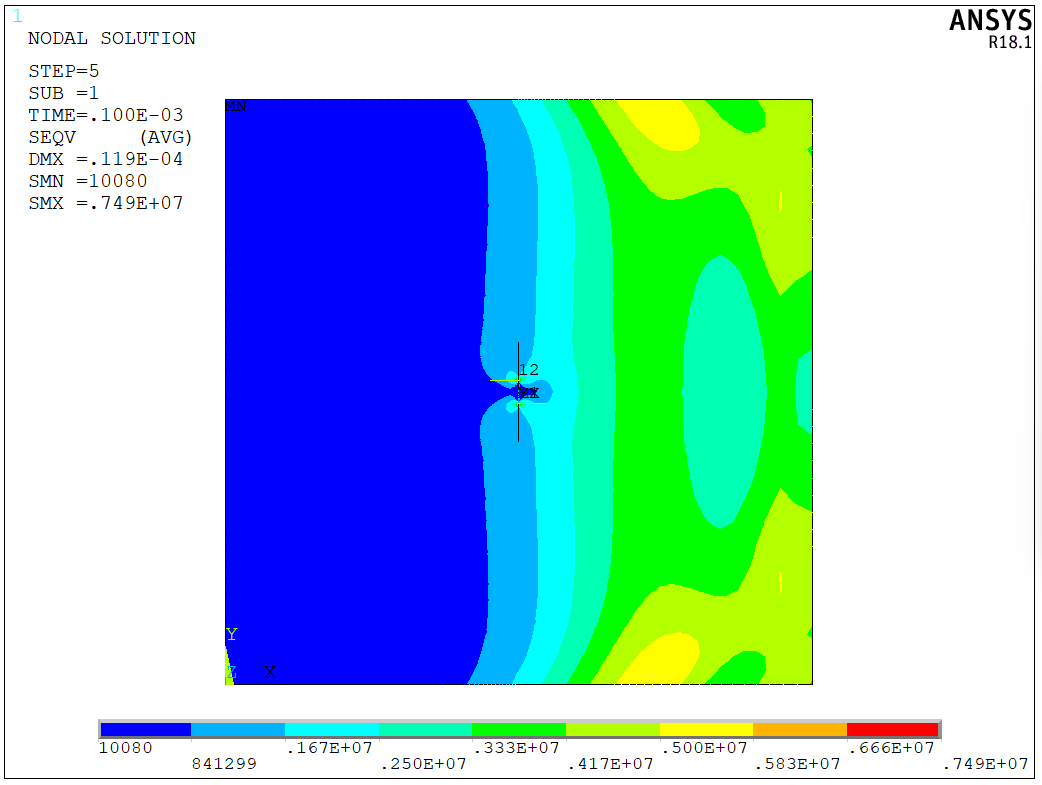
The results related to stress distribution are shown in the following figures (stress distribution at T = 1E-4, 1E-3, and 2E-2 s),
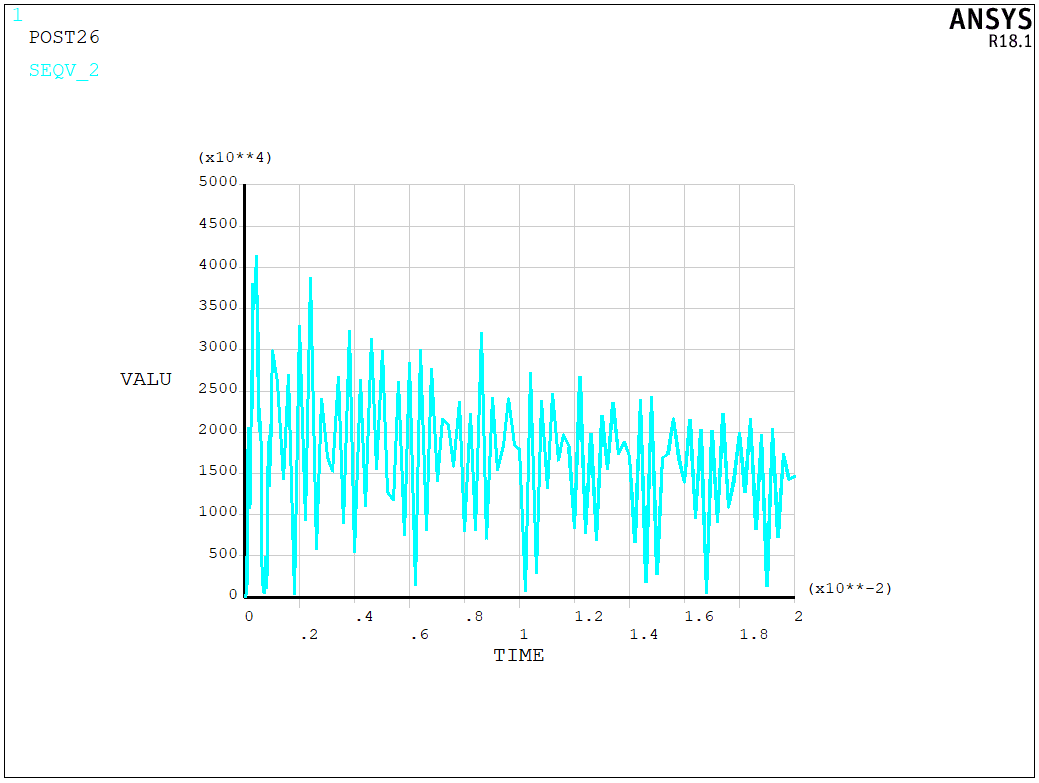
We can also plot the crack tip stress evolution with respect to time,
Since we store the SIFs into the array, it is easy to save it to the local file by VWRITE command and here are the results,
The model is a test model, and the APDL code is available upon request.