Mathematica image matching and coordiate extraction

Posted on | In

Mathematica Previously, due to some requirements, I need to extract coordinate data from a deformed image and found that Mathematica can indeed do a lot of things. So, I combined information from forums and help documents to see if there was anything interesting to explore. I discovered that Mathematica can perform image matching, and thus I wanted to use Mathematica image matching to locate the position of a small part of an image within a larger image.

While Mathematica image matching function can match images, it does not return positions. This requires manual intervention. I searched Google and found that indeed, someone had asked about this on an Mathematica forum. However, this method didn’t fully solve our problem because, I found that this method wasn’t great enough and had certain flaws through my experiments. It seems that to achieve a better method of extracting coordinates, we have to take matters into our own hands.

Basic knowledge

Image coordinate issues in Mathematica

In Mathematica, the origin of an image is at the bottom left corner, similar to the usual coordinate system. However, in some programming languages, the origin is at the top left corner, which can cause confusion. It’s important to remember this first.

ImageData function

This function extracts pixel information and color information from an image. It extracts the coordinates of pixels with color information. However, this function scans pixel information from top to bottom, so we need to understand this matrix. I’ll use the following image as an example,

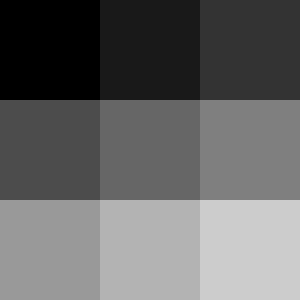
Mathematica image matching

In Mathematica, standardized raster data considers 0 as black and 1 as white. Therefore, when we use ImageData to obtain this image data, we can get the following matrix,

\[\left[ {\begin{array}{cc} 0&{0.1}&{0.2}\\ {0.3}&{0.4}&{0.5}\\ {0.6}&{0.7}&{0.8} \end{array}} \right]\]

If we use the Position[] function to extract the location of a pixel with a color value of 0.2, the data obtained would be (1,3), which is equivalent to calculating this pixel coordinate position from the top left corner of the image. This is different from Mathematica default coordinate position, so it needs to be noted.

Image Matching

After the above basic analysis, we can start this task. We first obtain a original image,

Mathematica image matching

This image was randomly selected from Dmitriy Me2dev’s photography works on Unsplash. Then we obtain a part of it,

Mathematica image matching

The question then arises, from which part of the original image does this small image come? If we closely compare the image, we might find the exact location, but this would be a huge amount of work. We can achieve image matching using the image matching function provided by Mathematica. First, we rename the original image as origin.jpg, and the part of the image as part.jpg. Then we directly use the following command for image matching,

1
2
3
4
origin = Import[NotebookDirectory[] <> "origin.jpg"]
part = Import[NotebookDirectory[] <> "part.jpg"]
comp = ImageAlign[origin, part]
ImageCompose[comp, {origin, .5}]

After image matching, we can get the following image,

Mathematica image matching

We can quickly find the location of this part of the image, but now the question is, how do we extract this specific location?

Obtaining Coordinates

First, we need to analyze the obtained image, which is a four-channel RGB image with an Alpha channel. We can see this when right-clicking to view the image information,

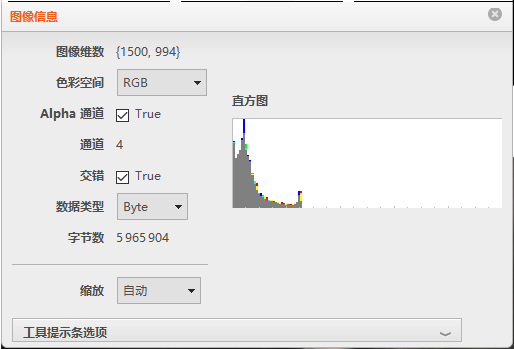
Mathematica image matching

For us, this image might not be very useful, but the composite channel is very useful. We need to obtain this channel image,

1
pos = ColorSeparate[comp]

With the above command, the image will be separated into color channels, resulting in four channels, the last of which is the Alpha channel image we need,

Mathematica image matching

With this channel image, we can extract the coordinates of all white points using the Position[] function and then obtain the minimum value,

1
2
cood = Position[ImageData[pos[[4]]], 1.];
min = Min /@ Transpose[cood]

A coordinate value can be directly obtained: (641, 874). Based on the basic knowledge mentioned above, this point is the top left corner of the white block, i.e., the pixel coordinate from the top down at the 641st row and 874th column. With some conversions, we obtain the bottom left corner pixel coordinate of the white block,

1
min = {min[[2]], ImageDimensions[origin][[2]] - min[[1]]}

This allows us to obtain the bottom left corner coordinates of the white block as: (874, 353). Highlighting this area on the image,

1
HighlightImage[origin, Rectangle[{min[[1]], min[[2]] - ImageDimensions[part][[2]]}, {min[[1]] + ImageDimensions[part][[1]], min[[2]]}]]

Mathematica image matching

With this, we have completed the work of extracting coordinates after image matching.

Conclusion

While this task seems simple, making it completely right still requires some time. When there is no reference material available, the help documentation becomes the best resource, even though the help can sometimes be too simplistic, requiring us to explore bit by bit. The reference can be found here: LINK.

The full script can be downloaded here: DOWNLOAD