The vector space $ \mathbb{V} $ with the operation (+) over a field of real number $ \mathbb{R} $ is an abelian group with a scalar multiplication. So, suppose $ \boldsymbol{x} $, $ \boldsymbol{y} $ and $ \boldsymbol{z} \in \mathbb{V}$, they satisfy the following conditions:
Abelian group:
- Closure:$ \boldsymbol{x} + \boldsymbol{y} \in \mathbb{V}$,
- Associativity: $ ( \boldsymbol{x} + \boldsymbol{y} )+ \boldsymbol{z}= \boldsymbol{y} + ( \boldsymbol{x}+ \boldsymbol{z} ) $,
- Identity: $ \exists \boldsymbol{0} \in \mathbb{V}, \forall \boldsymbol{x} \in \mathbb{V} $ such that $ \boldsymbol{0} + \boldsymbol{x} = \boldsymbol{x} $ and $ \boldsymbol{x} + \boldsymbol{0} = \boldsymbol{x} $,
- Invertibility $ \exists ! ( -\boldsymbol{x} ) \in \mathbb{V}, \forall \boldsymbol{x} \in \mathbb{V} $ such that $ ( -\boldsymbol{x} ) + \boldsymbol{x} = \boldsymbol{0} $ and $ \boldsymbol{x} + ( -\boldsymbol{x} ) = \boldsymbol{0} $,
- Commutativity: $ \boldsymbol{x} + \boldsymbol{y} = \boldsymbol{y} + \boldsymbol{x} $.
Scalar multiplication:
- $ \forall \alpha, \beta \in \mathbb{R} $, $ \forall \boldsymbol{x} \in \mathbb{V} $ such that $ ( \alpha \beta ) \boldsymbol{x} = \alpha ( \beta \boldsymbol{x} ) $,
- $\forall \alpha, \beta \in \mathbb{R} $, $ \forall \boldsymbol{x}, \boldsymbol{y} \in \mathbb{V} $ such that $ \alpha ( \boldsymbol{x} + \boldsymbol{y} ) = \alpha \boldsymbol{x} + \alpha \boldsymbol{y} $ and $ ( \alpha + \beta ) \boldsymbol{x} = \alpha \boldsymbol{x} + \beta \boldsymbol{x} $,
- $ 1 \boldsymbol{x} = \boldsymbol{x} $.
This is not a tutorial, please refer to the books for tensor algebra.
Linearly independent:
For a set of non-zero vectors $ {\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, \dots, \boldsymbol{x}_n, }$, $ \exists \alpha_1, \alpha_2, \alpha_3, \dots, \alpha_n \in \mathbb{R}$, such that,
\[\displaystyle \sum_{i=1}^n \alpha_i \boldsymbol{x}_i = \boldsymbol{0}\]if and only if $ \alpha_1, \alpha_2, \alpha_3, \dots, \alpha_n = 0 $.
Such set of the vectors $ {\boldsymbol{x}_1, \boldsymbol{x}_2, \boldsymbol{x}_3, \dots, \boldsymbol{x}_n, }$ is called linearly independent.
Vector space dimension:
Let $ \mathcal{G} = {\boldsymbol{g}_1, \boldsymbol{g}_2, \boldsymbol{g}_3,\dots,\boldsymbol{g}_n }$ be a subset of a vector space $ \mathbb{V}$ and $latex \alpha_i \in \mathbb{R}$, the vector,
\[\displaystyle \boldsymbol{x} = \sum_{i=1}^n \alpha_i \boldsymbol{g}_i\]is the linear combination of the vectors $ {\boldsymbol{g}_1, \boldsymbol{g}_2, \boldsymbol{g}_3,\dots,\boldsymbol{g}_n }$.
With the definition of the linear combination, the vector space dimension can be defined: A set $\mathcal{G} \subset \mathbb{V}$ of linearly independent vectors is a basis of a vector space $ \mathbb{V}$ if every vector in $ \mathbb{V}$ is the linear combination of the elements in $ \mathcal{G}$.
Theorem: All the basis of a finite-dimensional vector space $ \mathbb{V}$ contains the same number of vectors.
Theorem: For a n-dimension vector space $ \mathbb{V}$, every set contains n linearly independent vectors is a basis of $\mathbb{V}$, every set contains more than n vectors is linearly dependent.
Summation convention:
Let $ \mathcal{G} = {\boldsymbol{g}_1, \boldsymbol{g}_2, \boldsymbol{g}_3,\dots,\boldsymbol{g}_n }$ be the basis of the vector space $ \mathbb{V}$, any vector in such space can be represented with the linear combination of the basis,
\[\displaystyle \boldsymbol{x} = \sum_{i=1}^{n} x^i \boldsymbol{g}_i = x^i \boldsymbol{g}_i\]The expression is shorten without the summation symbol. This is called the Einstein summation. As shown on the mathworld, there are three rules of this notational convention:
- Repeated indices are implicitly summed over,
- Each index can appear at most twice in any term,
- Each term must contain identical non-repeated indices.
Theorem: The representation of the vector in the vector space $\mathbb{V} $ with respect to a given basis $\mathcal{G}$ is unique.
Euclidean space:
Suppose $ \boldsymbol{x} $, $ \boldsymbol{y} $ and $ \boldsymbol{z} \in \mathbb{V}$, then the vector space $ \mathbb{V}$ with inner product of the vectors satisfying the following conditions is called Euclidean space $ \mathbb{E}^n$ :
- Commutativity: $ \boldsymbol{x} \cdot \boldsymbol{y} = \boldsymbol{y} \cdot \boldsymbol{x}$,
- Distributivity: $ \boldsymbol{x} \cdot ( \boldsymbol{y} + \boldsymbol{z}) = \boldsymbol{x} \cdot \boldsymbol{y} + \boldsymbol{x} \cdot \boldsymbol{z} $,
- Associativity with a scalar: $ \alpha (\boldsymbol{x} \cdot \boldsymbol{y}) = (\alpha \boldsymbol{x}) \cdot \boldsymbol{y} = \boldsymbol{x} \cdot (\alpha \boldsymbol{y})$,
- $ \boldsymbol{x} \cdot \boldsymbol{x} \ge 0, \forall \boldsymbol{x} \in \mathbb{V}$, $ \boldsymbol{x} \cdot \boldsymbol{x} = 0$ if and only if $ \boldsymbol{x} = 0$.
Since the inner product of the vectors in $ \mathbb{E}^n$ is non-negative, the Euclidean distance or length (Norm) is defined by,
\[\displaystyle \|x\|=\sqrt{\boldsymbol{x} \cdot \boldsymbol{x}}\]Orthonormal basis:
- Orthogonal: $ \boldsymbol{x} \cdot \boldsymbol{y} = 0$,
- Normal: $ |x|=1$.
Let $ \mathcal{E} = {\boldsymbol{e}_1, \boldsymbol{e}_2, \boldsymbol{e}_3, \dots, \boldsymbol{e}_n }$ be a basis of $ \mathbb{V}$, if $ \forall \boldsymbol{e}_i, \boldsymbol{e}_j \in \mathcal{E}$ satisfy the preceding conditions, then the set $ \mathcal{E}^n$ is called orthonormal basis, i.e.
\[\displaystyle \boldsymbol{e}_i \cdot \boldsymbol{e}_j = \delta_{ij} ,i,j = 1, 2, 3, \dots, n\]The symbol is called Kronecker delta,
\[\displaystyle \delta_{ij}=\delta^{ij}=\delta^i_j=\begin{cases} 1 & \text{if}\ i = j\\ 0 & \text{if}\ i \ne j \end{cases}\]Every set of linearly independent vectors in Euclidean space $ \mathbb{E}^n$ can be orthogonalized and normalized with the Gram-Schmidt procedure.
Dual basis:
The dual basis of vectors is a biorthogonal system of the original basis of vectors in vector space $ \mathbb{V}$, the detail information can be found in wikipedia. It is a little bit abstract, the following figure shows the original basis $ { \boldsymbol{g}_1, \boldsymbol{g}_2 }$ and the dual basis $ { \boldsymbol{g}^1, \boldsymbol{g}^2 }$ in 2D Euclidean space $ \mathbb{E}^2$.
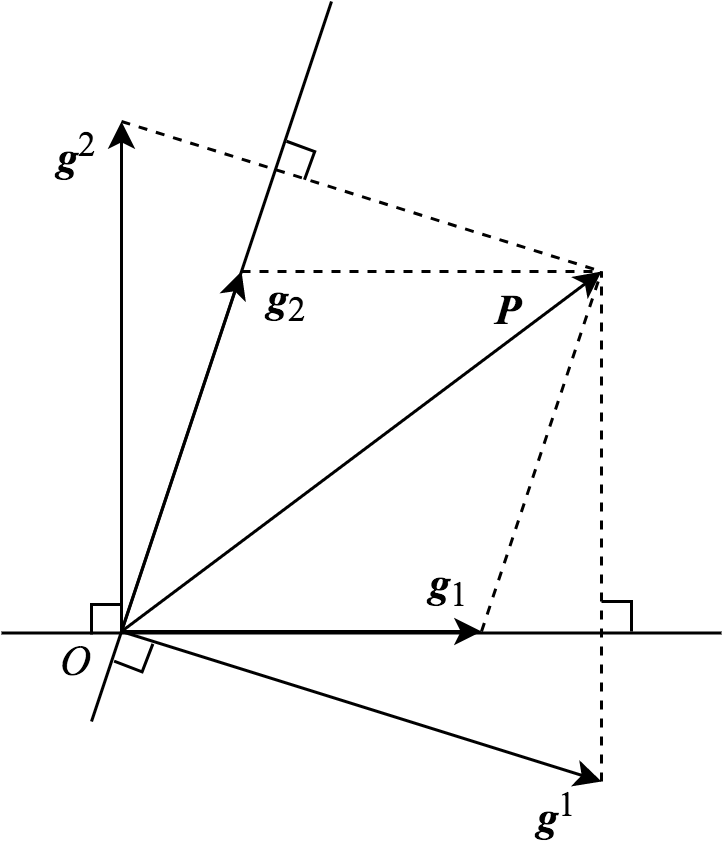
In this figure, $ \boldsymbol{g}_i \cdot \boldsymbol{g}^j = \delta_i^j$. Now, extend the 2D Euclidean space $ \mathbb{E}^2$ to nD Euclidean space $ \mathbb{E}^n$, the basis $ \mathcal{G}^ \prime = {\boldsymbol{g}^1, \boldsymbol{g}^2, \boldsymbol{g}^3, \dots,\boldsymbol{g}^n }$ is the dual basis to the basis $ \mathcal{G} = {\boldsymbol{g}_1, \boldsymbol{g}_2, \boldsymbol{g}_3, \dots,\boldsymbol{g}_n }$, if that,
\[\displaystyle \boldsymbol{g}_i \cdot \boldsymbol{g}^j = \delta_i^j \quad i,j = 1, 2, 3, \dots, n\]Theorem: There exists a unique dual basis of each basis in an Euclidean space $ \mathbb{E}^n$.
Proof: Let $ \mathcal{G}^ \prime = {\boldsymbol{g}^1, \boldsymbol{g}^2, \boldsymbol{g}^3, \dots,\boldsymbol{g}^n }$ and $ \mathcal{H}^ \prime = {\boldsymbol{h}^1, \boldsymbol{h}^2, \boldsymbol{h}^3, \dots,\boldsymbol{g}^n }$ be the two dual bases of the original basis $ \mathcal{G} = {\boldsymbol{g}_1, \boldsymbol{g}_2, \boldsymbol{g}_3, \dots,\boldsymbol{g}_n }$, recall the properties of the dual basis, \(\displaystyle \boldsymbol{g}_i \cdot \boldsymbol{g}^j = \delta^j_i\) \(\displaystyle \boldsymbol{g}_i \cdot \boldsymbol{h}^j = \delta^j_i\) Expand $ \boldsymbol{h}^j = h^j_k \boldsymbol{g}^k$ we get, \(\displaystyle \delta^j_i = \boldsymbol{g}_i \cdot \boldsymbol{h}^j = \boldsymbol{g}_i \cdot (h^j_k \boldsymbol{g}^k) = h^j_k \delta_i^k = h^j_i\) Then, \(\displaystyle \boldsymbol{h}^j = h^j_k \boldsymbol{g}^k = \delta^j_i \boldsymbol{g}^k = \boldsymbol{g}^j\)
Now, let $ \boldsymbol{g}_i$ be the basis of $ \boldsymbol{g}^i$, then,
\[\displaystyle \boldsymbol{g}^i = g^{ij} \boldsymbol{g}_j\]Expend the $ \boldsymbol{g}_j$ with respect to the $ \boldsymbol{g}^j$, then,
\[\displaystyle \boldsymbol{g}_j = g_{jk} \boldsymbol{g}^k\]Thus,
\[\displaystyle \boldsymbol{g}^i = g^{ij} g_{jk} \boldsymbol{g}^k\] \[\displaystyle \boldsymbol{0} = g^{ij} g_{jk} \boldsymbol{g}^k - \boldsymbol{g}^i = (g^{ij} g_{jk} - \delta_k^i) \boldsymbol{g}^k\]we get,
\[\displaystyle g^{ij} g_{jk} = \delta_k^i\]Then, the matrices $ g^{ij} $ and $ g_{jk} $ (i.e. $ g_{ji} $) are inverse of each other.
Dual basis Properties:
For orthonormal basis of $ \mathbb{E}^n$, it is a self dual vector space,
\[\displaystyle \boldsymbol{e}_i = \boldsymbol{e}^i\] \[\displaystyle \boldsymbol{e}_i \cdot \boldsymbol{e}^j = \delta_i^j = \delta_{ij} = \boldsymbol{e}_i \cdot \boldsymbol{e}_j = \delta^{ij} = \boldsymbol{e}^i \cdot \boldsymbol{e}^j\]For non-orthonormal basis of $ \mathbb{V}$,
\[\displaystyle \boldsymbol{g}^i \cdot \boldsymbol{g}^j = \boldsymbol{g}^j \cdot \boldsymbol{g}^i = g^{ij} = g^{ji}\] \[\displaystyle \boldsymbol{g}_i \cdot \boldsymbol{g}_j = \boldsymbol{g}_j \cdot \boldsymbol{g}_i = g_{ij} = g_{ji}\]The inner product of vector $ \boldsymbol{x}$ and $ \boldsymbol{y}$,
\[\displaystyle \boldsymbol{x} \cdot \boldsymbol{y} = x^i \boldsymbol{g}_i \cdot y_j \boldsymbol{y}^j = x^i y_j \delta^j_i = x^i y_i = x^j y_j\]Levi-Civita symbol:
Levi-Civita symbol is the permutation symbol,
\[\displaystyle \varepsilon_{ijk} = \varepsilon^{ijk} = \begin{cases} 1 & \text{ if } ijk \text{ is an even permutation }\\ -1 & \text{ if } ijk \text{ is an odd permutation } \\ 0& \text{ if otherwise } \end{cases}\]- Even permutation: $ 123, 231, 312$,
- Odd permutation: $ 132, 321, 213$,
- Otherwise: more than two symbols are the same e.g. $ 112, 223, 333$.
Let $ {\boldsymbol{e}_1, \boldsymbol{e}_2, \boldsymbol{e}_3 }$ be the orthonormal vectors in $ \mathbb{E}^3$ and [ ] be the symbol of mixed product of three vectors,
\[\displaystyle \varepsilon_{ijk} = [\boldsymbol{e}_i \boldsymbol{e}_j \boldsymbol{e}_k], \quad i, j, k = 1,2,3\]Denote g as the result for mixed product of basis vectors $ {\boldsymbol{g}_1, \boldsymbol{g}_2, \boldsymbol{g}_3}$ in $ \mathbb{E}^3$,
\[\displaystyle g = [ \boldsymbol{g}_1 \boldsymbol{g}_2 \boldsymbol{g}_3] = [ \beta^i_1 \beta^j_2 \beta^k_3 \boldsymbol{e}_i \boldsymbol{e}_j \boldsymbol{e}_k] = \beta^i_1 \beta^j_2 \beta^k_3 [ \boldsymbol{e}_i \boldsymbol{e}_j \boldsymbol{e}_k] = \beta^i_1 \beta^j_2 \beta^k_3 \varepsilon_{ijk}\]The last term $ \beta^i_1 \beta^j_2 \beta^k_3 \varepsilon_{ijk} $ is the determinant of the matrix i.e. $ g = \textbf{Det}[\beta^i_j]$,
Since we get,
\[\displaystyle g_{ij} = \boldsymbol{g}_i \cdot \boldsymbol{g}_j = \beta_i^k \boldsymbol{e}_k \cdot \beta_j^l \boldsymbol{e}_l = \beta_i^k \beta_j^l \delta_{kl} = \beta_i^k \beta_j^k\]Thus,
\[\displaystyle |g_{ij}| = \textbf{Det}[g_{ij}] = \|[\beta_i^k][\beta_j^k]\| = \textbf{Det}[\beta^i_j]^2 = g^2\]Levi-Civita symbol properties:
\[\displaystyle \varepsilon_{ijk} \varepsilon^{imn}=\delta_j^{m}\delta_k^n - \delta_j^n\delta_k^m\] \[\displaystyle \varepsilon_{jmn} \varepsilon^{imn}=2 \delta_j^i\] \[\displaystyle \varepsilon_{ijk} \varepsilon^{ijk}= 6\] \[\varepsilon_{ijk} \varepsilon_{lmn} = \delta_{il} ( \delta_{jm}\delta_{kn} - \delta_{jn} \delta_{km}) - \delta_{im} ( \delta_{jl} \delta_{kn} - \delta_{jn} \delta_{kl} ) + \delta_{in} ( \delta_{jl} \delta_{km} - \delta_{jm} \delta_{kl})\]Mixed product (triple product):
With the permutation symbol, the mixed product can be expressed by,
\[\displaystyle \varepsilon_{ijk}g = [\boldsymbol{g}_i \boldsymbol{g}_j \boldsymbol{g}_k] = \boldsymbol{g}_i \cdot (\boldsymbol{g}_j \times \boldsymbol{g}_k)\]then multiplying both sides of this relation by the vector $ \boldsymbol{g}^i$
\[\displaystyle \varepsilon_{ijk}g \boldsymbol{g}^i = \boldsymbol{g}_j \times \boldsymbol{g}_k\]
Since $ \textbf{Det}[\boldsymbol{g}_i \cdot \boldsymbol{g}^j] = \textbf{Det}[\delta_i^j]=1$,
\[\displaystyle 1= \textbf{Det}[\boldsymbol{g}_i \cdot \boldsymbol{g}^j] = \textbf{Det}[\boldsymbol{g}_i \cdot g^{jk} \boldsymbol{g}_k] = \textbf{Det}[g_{jk}] \textbf{Det}[g^{ik}]\]Then we get,
\[\displaystyle |g^{ik}| = \frac{1} {|g_{jk}|} \leftrightarrow |g^{ij}| = \frac{1} {|g_{ij}|} = \frac{1}{g^2} = \frac{1}{[\boldsymbol{g}_1 \boldsymbol{g}_2 \boldsymbol{g}_3]^2}\]Thus,
\[\displaystyle \frac{\varepsilon_{ijk}}{g} \boldsymbol{g}_i = \boldsymbol{g}^j \times \boldsymbol{g}^k\]
Then,
\[\displaystyle \boldsymbol{a} \times \boldsymbol{b} = (a^i \boldsymbol{g}_i)\times(a^j \boldsymbol{g}_j) = \varepsilon_{ijk} a^i b^j g \boldsymbol{g}^k=g\begin{vmatrix} a^1 &a^2 &a^3 \\ b^1 &b^2 &b^3 \\ \boldsymbol{g}^1 &\boldsymbol{g}^2 &\boldsymbol{g}^3 \end{vmatrix}\] \[\displaystyle \boldsymbol{a} \times \boldsymbol{b} = (a_i \boldsymbol{g}^i)\times(a_j \boldsymbol{g}^j) = \varepsilon^{ijk} a_i b_j \frac{1}{g} \boldsymbol{g}_k=\frac{1}{g} \begin{vmatrix} a_1 &a_2 &a_3 \\ b_1 &b_2 &b_3 \\ \boldsymbol{g}_1 &\boldsymbol{g}_2 &\boldsymbol{g}_3 \end{vmatrix}\]For 3D Euclidean space $ \mathbb{E}^3$, $ g = 1$, the cross product is,
\[\displaystyle \boldsymbol{a} \times \boldsymbol{b} = \begin{vmatrix} a_1 &a_2 &a_3 \\ b_1 &b_2 &b_3 \\ \boldsymbol{e}_1 &\boldsymbol{e}_2 &\boldsymbol{e}_3 \end{vmatrix}\]